고체의 결정구조 : 에너지 밴드
반도체의 정의를 말하라고 하면 일반적으로 도체나 부도체의 중간에 있는 물질이라는, 고등 교육과정에서 배운 이야기가 먼저 떠오르실 겁니다. 그러나 이러한 애매모호한 정의는, 700조원 규모의 산업을 세우는 토대로써는, 약간 부실하게 느껴집니다. 사실 우리는 반도체를 실생활에서 과학적 정의만으로 사용하지 않고, 정말 규소와 같은 반도체로 분류되는 물질부터 패키징이 완료된 반도체 칩까지 모두 반도체라고 부르고 있습니다. 자연스레 사람마다 어떤 관점으로 반도체를 보는지에 따라 정의가 다양하게 나뉘겠지만, 이 블로그에서는 먼저 반도체 물성의 관점에서, 기초부터 반도체를 이해해 나가고자 합니다. 반도체 공학도로써, 물성적 관점에서 반도체를 가장 잘 설명하는 것은 "온도에 따라 전도도 특성이 극도로 바뀌는 물질" 이라고 생각합니다. 이 정의를 제대로 알기 위해서는, 고체의 에너지 밴드 이론을 이해해야 합니다.

원자 내 전자의 배치는 주양자수, 각운동량 양자수, 자기 양자수, 스핀양자수 등등 다양한 양자수의 조합으로 이루어집니다. 현대물리에서 사용되는 이런 개념들을 간단히 짚고 넘어가자면,
주양자수 : 오비탈의 에너지 레벨 결정
각운동량 양자수 : 주양자수의 에너지 레벨 세분화, 오비탈 모양 결정
자기 양자수 : 같은 주양자수와 각운동량 양자수 내 오비탈의 방위 결정
양자역학적인 해석을 거쳐 나온 결과이고, 수소 원자 이상은 제대로 해석조차 힘든 복잡한 내용이지만 , 결국 우리는 각 전자가 "주어진 양자수에 따라, 특정 에너지 수준을 유지하고 있다" 라는 것만 가져가시면 됩니다. 즉, 진공 에너지를 0으로 둘때, 모든 우주의 수소 원자에서 주양자수 2, 각운동량 양자수 1을 차지하는 전자는 -3.4eV 의 에너지를 가진다는 것입니다.

또한 우리는 현대물리에서 파울리의 배타 원리라는, 같은 양자상태를 가진 페르미온은 중첩되지 못한다는 것을 알 수 있습니다. 그렇다면, 원자들이 고체를 이뤄 입자 간 거리가 가까워지고, 오비탈이 중첩된다면 이 전자들은 어떻게 될까요?
오른쪽 그림에서 보듯이, 고체 내에서 중첩된 에너지 준위는 위아래로 약간씩 "밀리고", 고체 내 수백 개의 원자들 사이에서 준위가 겹친다면 이는 연속된 띠 형태를 이루게 됩니다. 이것이 고체물리학의 기본이 되는, 밴드 이론입니다. 그러면 저 밴드에는 전자가 가득 들어있는 것일까요? 위 그림에서만 보이는 수소 원자의 오비탈만 16개인데, 그럴 리가 없겠죠. 밴드에 입자가 분포되는 것은 페르미 디락 통계를 따릅니다.

페르미 대락 통계는 간단하게 특정 온도, 특정 에너지에서 전자가 발견될 확률을 알려주는 함수입니다. 전자가 발견될 확률이 50%인 페르미 에너지라 불리는 특정 에너지를 중심으로 급격하게 감소하여 낮은 에너지로 갈수록 전자의 발견 확률이 1, 높은 에너지로 갈수록 발견 확률이 0에 수렴합니다. 위 밴드구조 그림에서 낮은 에너지 준위의 2s 오비탈과 높은 에너지 준위의 2p 오비탈이 밴드 구조를 이루며 겹치는 것을 볼 수 있는데, 항상 아래 준위와 위 준위가 겹쳐지는 것은 아닙니다. 할당된 에너지 준위가 없어 전자가 존재할 수 없는 에너지 레벨을 밴드갭이라고 하는데, 밴드갭이 없어서 모든 에너지 레벨에서 전자 발견 확률이 페르미 디락 통계를 따르는 물질을 도체라고 합니다.
또한 페르미 디락 통계 그래프를 보면, 온도에 따라 분포 그래프가 점점 완만해집니다. 밴드갭이 커서 확률이 1과 0으로 수렴하는 구간에만 전자가 채워질 수 있는 에너지 밴드가 존재한다면, 그런 물질은 온도에 상관없이 전자 (혹은 정공) 이 거의 존재하지 않고 전기 전도가 힘들 것입니다. 이런 물질을 부도체라고 합니다. 그러나, 페르미 준위를 기준으로 에너지 밴드가 애매한 거리만큼 떨어져 있다면 그런 물질은 온도 차이에 의해 전도도가 크게 뒤바뀔 것이고, 이런 물질들을 우리는 주로 반도체로 활용합니다. 밴드갭에 페르미 에너지가 위치해 있을 때, 밴드갭이 5eV 이상인 물질을 부도체로 분류합니다.
고체의 에너지 밴드 구조
양자역학적으로, 파울리의 식은 어떤 양자상태에 입자가 존재할 확률을 나타낸다. 그러나 파울리의 배타율 때문에 공간 내 양자상태는 제한되어 있고, 실제 전자 수를 계산하기 위해서는 공간 내 허용 에너지 상태들을, (파울리의 식을 활용하기 위해) 에너지의 함수로 표현하여야 하는데 이를 에너지 상태밀도 함수 (Energy Density of State function, DOS) 라고 합니다.
상자 안의 슈뢰딩거 방정식의 해를 구하고, 이를 운동량과 엮어서 계산하면 (E-k 관계 이용)

형태의 식이 나옵니다. 식은 에너지의 제곱근에 비례하여 상태밀도가 많아지며
(이는 dk 가 E의 루트에 비례하여 증가, 상태밀도는 k-공간내 구 표면적으로 k^2 - 에너지에 비례해서 증가
상태밀도를 나타내는 구의 shell 은 E 에 비례하여 넓어지는데, 단위 에너지의 루트에 비례하여 shell 을 미분하여야 그렇게 됨)
질량의 3/2 승에 비례한다는 것을 알 수 있습니다.

전도대의 경우 식은 유효질량을 활용하여(유효질량의 개념은 차후 설명하겠습니다) 좌측과 같이 바뀝니다. 이를 페르미 디락함수와 적절하게 합치면 그림과 같은 식이 나오는데, 이것이 평형상태의 허용 밴드 내 carrier concentraion이 됩니다.
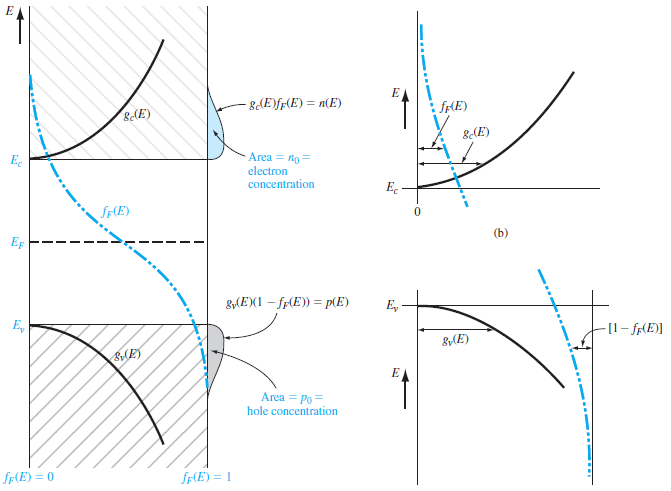

추가적으로, 위에서 Ec / Ev 로 상수 취급하였던 밴드갭 역시 온도 변화에 의존적입니다. 이는 차후 설명할 격자 구조가 온도에 따라 변하기 때문에 일어나는 현상입니다.
기본적인 고체물리와 연관된 내용은 수학적인 증명과정 없이 풀어내는 것이 쉽지 않습니다. 그러나, 반도체를 공부함에 있어 몇 가지 요소들은 기억해 두시는 것이 좋습니다.
- 파울리 배타 원리에 의해, 개별 에너지 준위가 Band 구조를 형성한다
- DOS 와 fermi function 의 곱으로, Carrier concentration 이 정해진다
또한, 아래와 같은 사실들을 추가적으로 유추해 볼 수 있습니다
> Carrier concentration 은 Band edge 가 아닌 근방에서 최대값을 가진다
> 유효질량이 클수록 carrier 농도가 높을 가능성이 높다
> Fermi Energy 와 Conduction / Valence Band 거리가 가까워질수록, 전자 농도가 지수적으로 증가한다*